Vertex quantization in Omniforce Game Engine
The problem
While textures can be heavily mipmapped and contain just enough data encoded in a single pixel (especially with BC1/BC7 compression), meshes are a bit more complicated. To reduce VRAM bandwidth, we can use LODs. However, it is not the panacea - I still have tons of redundant data encoded in a single vertex. By “redundant” I mean either excessive data/precision (e.g. FP32-encoded normals) or some values/bits that don’t affect on final mesh at all, for example: I have a mesh that is 10 units in size (10 floats). Nonetheless, a single 32-bit float can represent values far beyond 10, meaning that we store redundant data, which can be compressed away.
The more vertices in some particular mesh we have, the more we need to wait until it is transferred to GPU caches, effectively increasing frame time. Another thing worth to mention - the more bytes a single vertex takes, the fewer vertices we can fit in a single cache line / entire cache, meaning that we would need 1. more reads and 2. more swaps in cache. If we are register-bound, compressing vertices can improve performance due to the fact that we have less data per vertex and we can fit more data in registers, especially with FP16 values.
Using the NVIDIA NSight Graphics profiler, I figured out that even with BC7-compressed textures I still don’t have enough L2 cache hit rates and VRAM usage could be lower. On the screenshot, it is visible that cache hits are 1. not consistent (maybe often cache swaps?) 2. are about 60% in general, meaning that about half of the time data is not found in the cache:

Renderer design considerations
From the very beginning of the development of my engine’s renderer, I wanted it to support highly detailed meshes. To make that possible, my renderer required a vertex compression system that not just quantizes vertex positions to 16-bit floats. I needed a higher compression ratio and a very fast, near-instant decoding algorithm alongside with minimal precision loss.
Another thing to consider is that my engine’s renderer is built around mesh shaders. This is a very important note, which will be used for position compression. On NVIDIA GPUs, FP16 and FP32 computing rates are the same starting from Ampere generation, however, I can benefit from it on Turing GPUs, where the FP16 computing rate is doubled compared to FP32 - this is one more thing to consider when designing compression system.
Meshes in my engine’s target scenes can have more than 200k polygons - which effectively proves my statement above about compression system requirements.
To summarize, I can highlight these features which have to be present in the quantization system:
- High compression rate, more than constant 50%
- Capability of runtime decoding
- Nearly instant decoding time
- Random access from Visibility Buffer
Implementation, part 1. Attribute compression
Normal compression
For normal encoding, I chose the good-old Octahedron-encoding method mentioned on this page by Krzysztof Narkowicz which turned out to be the best option among others. It works fairly simple - normals are unit vectors, hence they represent points on the unit sphere. The sphere can be divided into 8 “sections”, effectively forming an octahedron, which then gets unfolded to a 2D plane, meaning that we can use vec2 normals instead of vec3! For visualization, see the photo below.
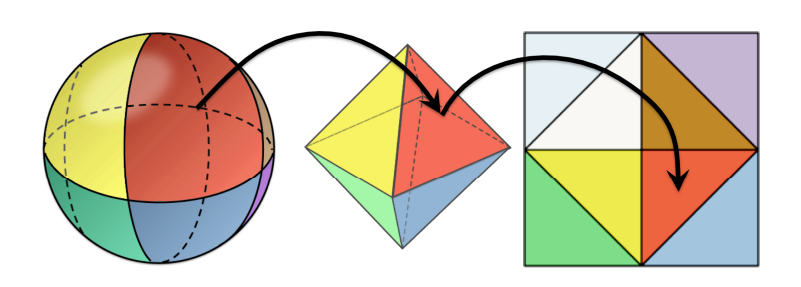
For further compression, I decided to compress vec2 which was returned after Octahedron encoding to 16-bit float. It takes some good bit of precision, but considering that most of the materials use 8-bit normal maps - I think that final precision loss is acceptable - it varied around 0.015. Using this method, I effectively compressed 12-byte vec3 normal to 4-byte fp16vec2 normal with acceptable precision loss.
To summarize:
- Use octahedron encoding with further compression to fp16
- Precision loss is approximately 0.015
- Decoding kept simple, nearly free
Encoding (C++, using GLM library for math):
glm::vec2 OctahedronWrap(glm::vec2 v) {
glm::vec2 w = 1.0f - glm::abs(glm::vec2(v.y, v.x));
if (v.x < 0.0f) w.x = -w.x;
if (v.y < 0.0f) w.y = -w.y;
return w;
}
glm::u16vec2 QuantizeNormal(glm::vec3 n) {
n /= (glm::abs(n.x) + glm::abs(n.y) + glm::abs(n.z));
n = glm::vec3(n.z > 0.0f ? glm::vec2(n.x, n.y) : OctahedronWrap(glm::vec2(n.x, n.y)), n.z);
n = glm::vec3(glm::vec2(n.x, n.y) * 0.5f + 0.5f, n.z);
return glm::packHalf(glm::vec2(n.x, n.y));
}
Decoding (GLSL)
#extension GL_EXT_shader_explicit_arithmetic_types_float16 : require
f16vec3 DecodeNormal(f16vec2 f)
{
f = f * 2.0hf - 1.0hf;
f16vec3 n = f16vec3(f.x, f.y, 1.0hf - abs(f.x) - abs(f.y));
float16_t t = max(-n.z, 0.0hf);
n.x += n.x >= 0.0hf ? -t : t;
n.y += n.y >= 0.0hf ? -t : t;
return normalize(n);
}
Tangent compression
As well as normals, tangents have multiple ways to be quantized. One of the options was using a single float32 or float16, describing an angle around normal. With such a method, decoding is done with Rodrigues’ Rotation Formula.
However, as I mentioned above - a very fast decoding time is one of the biggest requirements. Using this approach, I could describe a tangent as an angle, encoded in 16-bit float, but decoding would involve transcendental GPU operations (sin/cos), which I wanted to avoid as much as possible. Also, considering that such a method would only save 2 bytes per vertex compared to my implementation, I decided to go another way.
Tangents are regular unit vectors, as well as normal, which means that we can use the same encoding algorithm - Octahedron -> fp16! However, things get a little bit trickier when we also need to encode bitangent sign. Thankfully, the sign is just 2 values, meaning that it can be represented using a single bit. After a little research, I came up with a solution - encode that single bit into an octahedron-encoded tangent. Very important note: encode bitangent sign bit after octahedron and fp16 compression, because if I do it vice-versa, the sign bit can be lost due to compression. I chose the lowest bit of the Y component - according to the IEEE-754 float16 standard, it is the lowest bit of mantissa, meaning that it has the least influence on final precision. After my tests, I ended up with approximately 0.03 precision loss for tangents.
Decoding is fairly simple - just use the same method of decoding as we used for normals with one little difference - extract sign bit before decoding using this snippet of code: float16 sign = float16BitsToUint16(tangent.y) & 1us ? 1.0hf : -1.0hf
To summarize:
- Tangents are octahedron-encoded with further compression to fp16
- Bitangent sign bit is copied to the Y component’s lowest bit
- Precision loss is approximately 0.03
- Decoding is as simple as normal decoding with an extra step to extract the sign bit
Encoding code (C++)
glm::u16vec2 QuantizeTangent(glm::vec4 t) {
glm::u16vec2 q = QuantizeNormal(glm::vec3(t.x, t.y, t.z));
// If bitangent sign is positive, we set first bit of Y component to 1, otherwise (if it is negative) we set 0
q.y = t.w == 1.0f ? q.y | 1u : q.y & ~1u;
return q;
}
Decoding code (GLSL)
#extension GL_EXT_shader_explicit_arithmetic_types_float16 : require
#extension GL_EXT_shader_explicit_arithmetic_types_int16 : require
f16vec4 DecodeTangent(f16vec2 f)
{
f16vec4 t;
t.xyz = DecodeNormal(f);
// Check if lowest bit of Y's mantissa is set. If so, bitangent sign is positive, otherwise negative.
t.w = bool(float16BitsToUint16(f.y) & 1us) ? 1.0hf : -1.0hf;
return t;
}
UV compression
Texture coordinates are simply compressed to fp16. However, it may lead to some problems with texture sampling when used on meshes with tiled textures - for example, a terrain.
Implementation, part 2. Vertex position compression
Compared to attributes, vertex compression has much more space for creativity. When I was looking through “Deep dive into Nanite Virtualized Geometry” by Brian Karis, I was inspired by their vertex compression system, which is where I got the idea for my own implementation.
Why not naive fp16 compression? The answer is simple - it doesn’t suit almost any of my requirements: vertex size is still comparably big (16 bits per channel) and it has large errors with big meshes. I needed another, better way for vertex position compression.
When I was implementing my system, I kept in mind three factors:
- My renderer is cluster-based
- Float32 and float16 can represent values far beyond mesh AABB, which is redundant and only introduces additional “worthless” bits
- Do I really need byte-aligned data structures? (spoiler: no)
Grid quantization
Overview
Vertex quantization is done using a uniform grid, where each vertex gets snapped to it. Grid step is an option - it can be set to a value in the range of 4 to 16, which means that grid step varies from 1 / pow(2, 4) to 1 / pow(2, 16). Compression is done with this code: round(x * pow(2, grid_precision)), which returns us a signed integer representing the grid step count (essentially, a compressed value). See the photos below for a visualization of the quantization process.
Say, we have a grid with 0.001 step. Outlined range is redundant precision which should be compressed away by snapping to the grid. In next photo, we have a 1D vertex laying at 6.39342:

After compression against a grid with step of 0.001, our vertex lays perfectly on 6.393, containing no excessive precision which requires additional bits for encoding:

Avoiding geometry cracks
Considering that my renderer is cluster-based and uses mesh shading technology, my mesh is split up into “meshlets”. Compressing them naively may introduce cracks between them (see a photo below), which is unacceptable. To solve it, I needed to quantize all vertices, lods (if using meshlet-level lods), and all spatial data in general (for example, meshlets’ centers), against the same grid.

Precision and bit size
Using this method, precision is kept very high. Maximum error equals to grid step size divided by 2, due to rounding. To calculate the final bit size, I use this (pseudo-) code: ceil(log2(round(f * pow(2, precision))). For example, if I want to get the final bit size of 1D vertex at 5.0 quantized against an 8-bit grid, I do this: ceil(log2(round(5.0 * pow(2, 8))), which returns 11.
Encoding in meshlet-space
To compress vertices even further, I encode them in meshlet-space, instead of local space. It can save us a good 1-6 bits (3-5 on average) per vertex channel, depending on meshlet spatial size. Now, this is how I encode the vertex:
round((f - meshlet-center) * pow(2, precision)).
We can calculate new vertex bit size using this technique: let’s say, we still have a 1D vertex laying at 5.0 and now it belongs to a meshlet with center at 4.2. Now, to calculate the new bit size, I use this: ceil(log2(round((5.0 - 4.2) * pow(2, 8))), and it returns us 8 - which is 3 bits less than the previous result, meaning that we saved additional 3 bits per channel.
Important note: meshlet centers must be quantized as well in order to avoid geometry cracks between meshlets.
Bit stream
All this compression and 3-5 bits savings don’t make any sense if I still have byte-aligned data structures. I needed a data structure that is not aligned to a byte - I needed a bit stream.
Using a bit stream instead of an array of float32/float16/uint/int, I can compress vertices much more effectively, because not a single bit will be wasted: data is packed as much as possible. This technique turned out to work really well on GPU - I simply used a GPU bitstream reader to fetch vertex data. By providing an offset in bits and num of bits to read, the reader returns us a uint representing encoded value.
Considering that I deal with non-byte-aligned data, I can’t just load some value from the bit stream and expect it to have a sign. To solve this, I used a trick called “bit extend” mentioned here, which expands the sign bit, effectively restoring the sign of the value.
Per-meshlet bitrate
So far, I had a uniform bitrate for each vertex in every meshlet across all LODs, which worked well. However, this quantization system is designed for use in pair with per-meshlet LODs. Using Epic Games’ virtual geometry technology for meshlet-level levels of detail, each consecutive LOD will have spatially bigger meshlets, which will increase bitrate for all previous LODs’ meshlets, effectively eliminating the entire point of encoding in meshlet-space (due to the fact that LODmax meshlet(s) may be as big as source mesh).
To solve this problem, I decided to have a variable per-meshlet bitrate. Now, each meshlet has its own bitrate which equals to worst-case bitrate among meshlet vertices. It requires storing the bitrate of meshlet data, however, it is not an issue, since it can be easily packed in a single uint variable with vertex_count and triangle_count values.
Decoding
As mentioned in previous sections, I wanted decoding to be as fast as possible.
To decode, I needed to convert a signed encoded vertex to a float, divide it by pow(2, precision), and add the meshlet center to which the vertex belongs to transform a vertex from meshlet-space to local (mesh) space.
In my implementation, I use the GLSL built-in ldexp() function for the division of a float by POT - it basically adds a signed integer to the float’s exponent, effectively multiplying/dividing it by POT value.
Compression results
Considering that compression is done based on per-meshlet bitrate, it highly depends on such variables as: parameters passed to mesh clusterizer, desired precision, and overall mesh spatial size.
For the test, I quantized this pistol model using an 8-bit grid. Pistol is ~24 units (floats) in size. Results are:
- Uncompressed size in bytes: 335616
- Compressed size in bytes: 87808
- Rate: 3.82
- Grid precision: 8 bits
- Min precision loss: 0
- Max precision loss: 0.0019
Encoding (C++)
// Quantize with multiplication by pow(2, precision) with further rounding
// Preserve sign for bit extend
uint32 QuantizeVertexChannel(float32 f, uint32 local_bitrate, uint32 meshlet_bitrate) {
int32 v = std::round(f * (1u << local_bitrate));
uint32 result = v < 0 ? (1u << meshlet_bitrate) + v : v;
return result;
}
const uint32 vertex_bitrate = 8;
uint32 grid_size = 1u << vertex_bitrate;
uint32 meshlet_idx = 0;
for (auto& meshlet_bounds : mesh_lods[i].cull_data) {
uint32 meshlet_bitrate = std::clamp((uint32)std::ceil(std::log2(meshlet_bounds.radius * 2 * grid_size)), 1u, 32u); // we need diameter of a sphere, not radius
RenderableMeshlet& meshlet = mesh_lods[i].meshlets[meshlet_idx];
meshlet.vertex_bit_offset = vertex_stream->GetNumBitsUsed();
meshlet.bitrate = meshlet_bitrate;
meshlet_bounds.bounding_sphere_center = glm::round(meshlet_bounds.bounding_sphere_center * float32(grid_size)) / float32(grid_size);
uint32 base_vertex_offset = mesh_lods[i].meshlets[meshlet_idx].vertex_offset;
for (uint32 vertex_idx = 0; vertex_idx < meshlet.vertex_count; vertex_idx++) {
for(uint32 vertex_channel = 0; vertex_channel < 3; vertex_channel++) {
float32 original_vertex = deinterleaved_vertex_data[base_vertex_offset + vertex_idx][vertex_channel];
float32 meshlet_space_value = original_vertex - meshlet_bounds.bounding_sphere_center[vertex_channel];
uint32 value = quantizer.QuantizeVertexChannel(
meshlet_space_value,
vertex_bitrate,
meshlet_bitrate
);
vertex_stream->Append(meshlet_bitrate, value);
}
}
meshlet_idx++;
}
Decoding (GLSL)
layout(buffer_reference, scalar, buffer_reference_align = 4) readonly buffer ReadOnlyBitStream {
uint storage[];
};
uint BitStreamRead(ReadOnlyBitStream bitstream, uint num_bits, uint bit_offset) {
uint value = 0;
// Optimization by using right shift instead of division by 32.
// Here I find uint cell index within a bit stream storage based on requested offset.
// It works because shifting to the right is equal to the division by value which is a power of 2.
uint index = bit_offset >> 5; // >> 5 instead of division by 32
// Optimization by using bit masking instead of modulo op.
// Here I find a bit offset within a single uint cell
// It works because I needed do find a 32 modulo of `data`, and 32 is 2^5,
// so I can simply bitmask all other bits except of first 4.
// This way only first 4 bits are left, which is the value I needed
uint local_offset = bit_offset & 0x1F;
// Create a bitmask based on local offset and num of bits to read,
// which will allow to read only necessary values from a cell
uint bitmask = ((1 << num_bits) - 1) << local_offset;
// Shift the read bits back to the beginning of a value
value = (bitstream.storage[index] & bitmask) >> local_offset;
// If value is not encoded entirely within a single cell, we need to do a second read from next cell
if (local_offset + num_bits > 32u) {
// Write new bitmask based on num of bits left to read
bitmask = ((1 << (num_bits - (32u - local_offset))) - 1);
// Read value using bitmask and shift it to the right, so values which were read by previous read are not overriden
value |= (bitstream.storage[index + 1] & bitmask) << (32u - local_offset);
}
return value;
}
vec3 DecodeVertex(const ivec3 encoded_vertex, int vertex_bitrate, const vec3 meshlet_center) {
return ldexp(vec3(encoded_vertex), ivec3(-vertex_bitrate)) + meshlet_center;
}
int RestoreSign(uint x, MeshletData meshlet_data) {
int bitmask = 1 << (meshlet_data.bitrate - 1);
return int((x ^ bitmask) - bitmask);
}
Performance tests
The final stage of my journey with quantization is profiling. With NVIDIA NSight Graphics, I managed to make 2 captures: with and without compression, each of them captured 3 frames using multi-pass metrics. Inputs were completely identical: the scene and its TRS are the same (Amazon Lumberyard Bistro Exterior), with identical camera settings and a full unlit scene.
Captures were made on NVIDIA GeForce GTX 1660 Ti GPU with Game Ready 552.12 driver. Metrics are compared to no quantization capture, not SOL. Results are:
- +25% L2 Read Hit Rate from L1
- +15% L2 Read Hit Rate
- +~10% L1TEX throughputs including texture-related ones (maybe affected by quantized UVs?).
- -15-20% VRAM bandwidth
- Slightly increased SM Instruction throughputs (~15-30%)
- -25% frame time: 2.1ms, down from 2.8ms.
Profiler screenshots (the first capture is no compression, the second is full compression):



Conclusion
This quantization system is definitely a win for my engine and almost perfectly fits my needs: high compression rate, fast decode and it works well with meshlet-level LODs. It impressively decreased my memory footprint, increased cache hit rates, and even lowered my frame time by 25% on average.
However, there is still a space for improvements:
- I assume that bitstream implementation can be optimized further. Nonetheless, I tried my best to squeeze the performance out of it
- Since normals and tangents are unit vectors even after compression, instead of storing unfolded octahedron’s “UV” in fp16 , I could extract 15-bit mantissa + 1 sign bit from each coordinate, effectively preserving much more precision. Yet I am not sure how complex would decoding be, so for now I left it as-is.
Thanks for reading!